Rubik's Cube - Wikipedia, the free encyclopedia: Rubik's Cube is a 3-D combination puzzle invented in 1974[1][2] by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube,[3] the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980[4] via German businessman Tibor Laczi and Seven Towns founder Tom Kremer,[5] and won the German Game of the Year special award for Best Puzzle that year. As of January 2009, 350 million cubes had been sold worldwide[6][7] making it the world's top-selling puzzle game.[8][9] It is widely considered to be the world's best-selling toy.[10]
In a classic Rubik's Cube, each of the six faces is covered by nine stickers, each of one of six solid colours: white, red, blue, orange, green, and yellow. In currently sold models, white is opposite yellow, blue is opposite green, and orange is opposite red, and the red, white and blue are arranged in that order in a clockwise arrangement.[11] On early cubes, the position of the colours varied from cube to cube.[12] An internal pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to consisting of one colour.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western safety and packaging specifications. A lighter Cube was produced, and Ideal decided to rename it. "The Gordian Knot" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many imitations and variations appeared.
Many Chinese companies produce copies of, and in some cases improvements upon, the Rubik and V-Cube designs. The most popular are Bao Daqing's DaYan company, who make the GuHong and ZhanChi and now PanShi models, amongst others. Although their legality is questionable, they are often preferred over the originals by expert speed cubers because of their ease of movement.{26]
However, the centre cube of each of the six faces is merely a single square façade; all six are affixed to the core mechanism. These provide structure for the other pieces to fit into and rotate around. So there are twenty-one pieces: a single core piece consisting of three intersecting axes holding the six centre squares in place but letting them rotate, and twenty smaller plastic pieces which fit into it to form the assembled puzzle.
Each of the six centre pieces pivots on a screw (fastener) held by the centre piece, a "3-D cross".
The Cube can be taken apart without much difficulty, typically by rotating the top layer by 45° and then prying one of its edge cubes away from the other two layers. Consequently it is a simple process to "solve" a Cube by taking it apart and reassembling it in a solved state.
There are six central pieces which show one coloured face, twelve edge pieces which show two coloured faces, and eight corner pieces which show three coloured faces. Each piece shows a unique colour combination, but not all combinations are present (for example, if red and orange are on opposite sides of the solved Cube, there is no edge piece with both red and orange sides). The location of these cubes relative to one another can be altered by twisting an outer third of the Cube 90°, 180° or 270°, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares. However, Cubes with alternative colour arrangements also exist; for example, with the yellow face opposite the green, the blue face opposite the white, and red and orange remaining opposite each other.
Douglas Hofstadter, in the July 1982 issue of Scientific American, pointed out that Cubes could be coloured in such a way as to emphasise the corners or edges, rather than the faces as the standard colouring does; but neither of these alternative colourings has ever become popular.[[
Permutations
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example,
The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysis. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence (i.e., permutations of the set of objects). This fact was known at least as early as the 12th century, to Indian scholars.[2] The notation n! was introduced by Christian Kramp in 1808.[3]
The definition of the factorial function can also be extended to non-integer arguments, while retaining its most important properties; this involves more advanced mathematics, notably techniques from mathematical analysis.
Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 37 (2,187) possibilities. There are 12!/2 (239,500,800) ways to arrange the edges, since an even permutation of the corners implies an even permutation of the edges as well. (When arrangements of centres are also permitted, as described below, the rule is that the combined arrangement of corners, edges, and centres must be an even permutation.) Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 211 (2,048) possibilities.[27]
The puzzle is often advertised as having only "billions" of positions, as the larger numbers are unfamiliar to many. To put this into perspective, if one had as many standard sized Rubik's Cubes as there are permutations, one could cover the Earth's surface 275 times.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large:










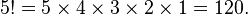
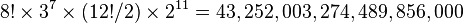

No comments:
Post a Comment